The game
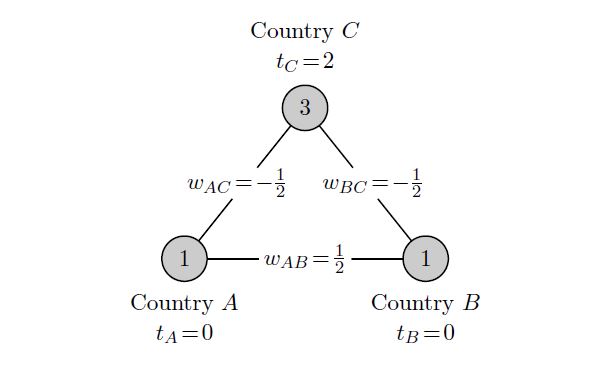
A weighted network game is described by a set of players who are situated at the nodes of a fixed network. Players make decisions about their economic activity: their level of production. The consumption benefits gained by each player depend on his own productivity and that of his neighbors in the network. Each link between two players is associated with a weight indicating how the production of a player at one endpoint of this link translates into additional consumption for the player at the other endpoint of this link. The weights describe the nature of the direct interactions between each pair of players with a positive weight indicating mutual direct benefits from each other's economic activity and a negative weight indicating mutual harm. Thus, the weighted network game offers a simple framework to model complex interactions between multiple decision-makers. Figure 1 provides an example.
Given the weighted network, players make production decisions using a linear production technology and each player benefits from his total consumption that equals his own production plus the weighted sum of his neighbors' productions. Each player has a target level, which is the level of consumption where the marginal consumption benefits equal the marginal cost of production. Given the production levels of the other players, a player's best response is to produce the target value minus the weighted sum of his opponents' productions (possibly bounded by the player's production possibilities). The situation presented in Figure 1 shows an equilibrium state where every player is at best response. We show that, apart from some knife-edge cases, a given weighted network game yields only a finite number of equilibrium situations.
Adaptive learning processes
The theory of learning is of fundamental importance in game theory. While a vast share of the non-cooperative game theory literature is devoted to the study of various equilibrium concepts, the main concepts - Nash equilibrium in particular - have proven difficult to validate. One of the main goals of learning in game theory is to understand in which cases and how an equilibrium is or can be reached, thereby providing validation of the equilibrium concept. This is typically achieved by obtaining the equilibrium as the outcome of a series of updates by the players playing the given game recurrently. Ideally, as the players discover more about the game and their opponents, their collective decisions should, in time, resemble equilibrium play.
We study a simple but rich class of learning processes in which, starting from some arbitrary production profile, players receive revision opportunities at discrete points in time. At any given period, only one player is allowed to update, making an adjustment that improves his own payoff. Such a process is called a better-response dynamic.
Intuitively, it seems clear that a single player acting in isolation, by making such improvements, will, in time, reach his optimal production level. The question we pose in this paper is whether this remains true for a setting with multiple players whose strategic interactions are described by a weighted network. One of the main difficulties in answering this question in the context of a multi-player setting is that, unlike in the one-player case, a player's revision changes the opponents' current optimal production decisions.
Structure of the game
Potential functions and their refinements try to capture all players' incentives by a single real-valued function. Such a single function is an exact potential if the change in any player's payoff from any given production profile by a change in this player's production level is
quantitatively perfectly captured by this function. It is an ordinal potential if these changes are only captured qualitatively, i.e., both increase or both decrease. Finally, it is a best-response potential if for any given production profile, an optimal change by a player also
leads to an optimal improvement of the function value.
We show that, while there does not generally exist an exact or an ordinal potential function, for every weighted network game there exists a best-response potential function. Additionally, this function is locally ordinal, meaning that small changes of a player's production level will change the player's payoff in the same direction as the function value.
Learning leads to equilibrium
The existence of a best-response potential means that best-response dynamics will not produce cycles. With weak additional assumptions, convergence to a Nash equilibrium can also be shown. However, we are interested in the behavior of better-response dynamics, a much more robust learning method as players are not required to necessarily choose best actions but only utility improving actions. Non-existence of an ordinal (or an exact) potential has as consequence that a better-response dynamic can produce cycles, an example of which is provided in the paper. Hence, for weighted network games, a better-response dynamic is not guaranteed to converge to a Nash equilibrium, without imposing additional restrictions.
We find that convergence of better-response dynamics to a Nash equilibrium is guaranteed as long as three conditions are satisfied.
1. Every single update may reach, or even overshoot the best-response of the updating player, but the distance to the best-response should not increase. This condition restricts the updates players make and guarantees that values of the best-response potential function are non-decreasing along every adaptive learning process.
2. There exists an amount of time such that every player revises at least once within that time span. This condition takes care of every player being able to revise regularly and ensures that no player gets stuck playing a suboptimal strategy by not being able to move often enough.
3. Weights and targets must be such that the game has a nite number of Nash equilibria. This condition concerns the game parameters and is required to ensure that convergence of the value of the best-response potential function does indeed lead to a convergence to an equilibrium. As mentioned earlier, this condition is satisfied for almost all weighted network games.
References
- Peter Bayer, P. Jean-Jacques Herings, Ronald Peeters and Frank Thuijsman (2019). Adaptive learning in weighted network games. Journal of Economic Dynamics and Control 105: 150-264. https://doi.org/10.1016/j.jedc.2019.06.004 [1].
About the Authors
Péter Bayer [2]is a postdoctoral researcher at Grenoble Applied Economics Lab of the University of Grenoble-Alpes. His current projects are on networks and the application of game theory to fight cancer. He received his PhD at Maastricht University in 2019 under the supervision of Jean-Jacques Herings, Ronald Peeters, and Frank Thuijsman. The title of his dissertation is "Public Goods Games on Networks and in Tumors". His research fields are networks, microeconomic theory, game theory and its applications.

Jean-Jacques Herings [3] is Professor of Microeconomics at Maastricht University’s School of Business and Economics. Herings has been at Maastricht University’s School of Business and Economics since 1999. He received his PhD from Tilburg University and previously worked as a post-doctoral fellow at the Catholic University of Louvain, as an associate professor at Tilburg University, and as a visiting professor at Yale University. Herings is a leading figure in several areas of economic theory including general equilibrium, both cooperative and non-cooperative game theory, (financial) networks, matching and computational economics. He has been recently elected Economic Theory Fellow by the Society for the Advancement of Economic Theory (SAET).
Ronald Peeters [4] is Professor and Associate Dean Research at the University of Otago. He obtained his PhD from Maastricht University in 2002, and has been working as assistant and associate professor in Maastricht until his move to Otago in October 2017. His research interests include game theory, behavioural economics, behavioural mechanism design and industrial organisation.
Frank Thuijsman [5] is professor of Strategic Optimization and Data Science at the Department of Data Science and Knowledge Engineering (DKE) of Maastricht University. For several years he has been Director of Studies for Knowledge Engineering and in 2014 he successfully launched the talent development program KnowledgeEngineering @ Work. His research is on (Evolutionary) Dynamic Game Theory, with a current focus on modeling tumor growth and cancer treatment. He has had visiting positions at the University of California at Los Angeles and at the Hebrew University of Jerusalem.