Time Banks: A Mechanism Design Approach

If a time bank is decentralized then it is reasonable to expect a bilateral exchange only to occur in case of a double coincidence of wants, i.e., a situation in which two individuals each want some service that the other person can provide. In case individuals only consider bilateral exchanges it can happen that no individual obtains any service. For instance, if we assume that agents can be associated with the (unique) service they can provide and that A only wants B, but B only needs C, and C only wants A, no bilateral trade exists.

There are two simple (and related) ways to avoid the requirement of double coincidence of wants. The first solution is the introduction of an explicit credit system. More specifically, providing (one hour of) a service gives one credit point, which can be used later to obtain a service from some other member of the community. The second solution is a clearing house that implicitly does the same thing by assigning to each member a service that she asks for in such a way that all credit points are obtained and spent simultaneously.
 

Housing markets

A basic time bank can be modelled through the classical “housing market” of Shapley and Scarf (1974), where each agent owns one indivisible good and monetary compensations are not possible. Each agent has preferences over all goods (including her own) and is interested in having exactly one good.

How could we achieve a “desirable” redistribution of the goods in the housing market, or equivalently, services in a time bank? According to the previous discussion it seems helpful to have a centralized clearing house that collects the agents’ preferences and uses them to implement an allocation. But would this be in the interest of the agents? Several concerns may arise. For instance, we would like to avoid that an agent receives an unacceptable good/service. We also would like to make sure that no further desirable trades are possible (as they could undermine the reputation of the clearing house). In other words, the clearing house should consider and exploit all possible trades among the agents. And finally, preference revelation should be simple and straightforward: if agents have to play a wicked strategic game in order to get desirable goods/services, then core values that underlie time banks are eroded.

In order to have a workable system in practice, we are interested in “rules”, i.e., systematic procedures that associate an allocation with each possible preference profile. A well-studied rule in this setting is David Gale's Top Trading Cycle (TTC) rule. This rule makes each individual “point” at her most preferred good, “implements” each cycle (i.e., assigns the most preferred good to each agent in a cycle), removes any cycles, and then repeats this process with the remaining agents/goods (and adjusted preferences). In the example mentioned earlier, the TTC rule immediately yields the cycle that consists of the three agents:

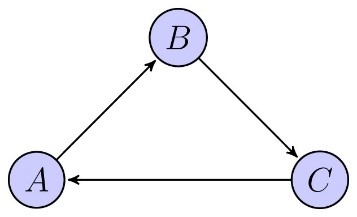
Roth and Postlewaite (1977) showed that for any profile of strict preferences, the TTC rule yields the unique (strong) “core” element. An important implication of their result is that the TTC rule is individually rational as well as Pareto-efficient. Individual rationality means that each individual always receives an acceptable good (possibly her own). Pareto-efficiency guarantees that there is never an alternative (re)distribution of the goods that makes everyone better off, i.e., the TTC rule is optimal in the sense that there do not exist welfare improvements through additional exchanges. Roth (1982) proved that the TTC rule is also strategy-proof, i.e., for each agent it is a weakly dominant strategy to reveal her true preferences. In other words, the TTC rule makes it a safe strategy to simply submit your true preferences—nothing can be gained by “cheating” or trying to set up some “smart” strategy. Another advantage of strategy-proofness is its fairness aspect as it levels the playing field: no agent (independently of her intellect or other types of resources) has a strategic advantage over any of the other agents. In short, in view of the three properties (individual rationality, Pareto-efficiency, and strategy-proofness) the TTC rule avoids the possible concerns that were mentioned earlier. So, the TTC rule is a satisfactory rule. Are there any other rules that “perform” similarly? The answer is negative: Ma (1994) showed that on the domain of strict preferences the TTC rule is the unique rule that satisfies individual rationality, Pareto-efficiency, and strategy-proofness.
 

Main assumptions

The framework of “housing markets” for time banks that we have discussed so far is basic in the sense that it is probably the simplest we can think of. It is based on several assumptions, (possibly the most obvious) three of which we discuss next. First, each agent is only interested in receiving and providing one service hour; formally, her “capacity” equals one. However, in a real-life time bank an agent could be interested in obtaining a bundle of services (possibly with multiple hours of the same service). Second, an agent could be able to provide more than one kind of service. For instance, maybe she could not only teach a foreign language, but could also mow a lawn. Third, an agent does not have preferences over (the identity of) the agent(s) that receive her service. While this seems a reasonable assumption for certain services such as mowing a lawn, it is clearly more problematic in the case of services that require substantial interaction such as babysitting or teaching a foreign language.
 

More general frameworks

Recent papers studied frameworks that relax the first assumption, i.e., agents could be interested in bundles of services (not just one unit of one particular service). In joint work with Péter Biró and Szilvia Pápai we studied a framework with general capacity configurations, assuming that agents have “responsive” preferences over bundles. Loosely speaking, responsiveness means that receiving more units of more preferred services at the expense of less preferred services yields more preferred bundles. The goal was again to find or design rules that for each possible preference profile yield a balanced allocation (or “circulation”), i.e., the total number/units/hours of services an agent receives equals the total number/units/hours of services an agent gives to the other agents.

Our first finding was that not every capacity configuration allows for an individually rational circulation rule that is both Pareto-efficient and strategy-proof.[i] However, we identified the (so-called “irreducible”) capacity configurations for which the three properties are compatible. The bad news is that the number and types of irreducible capacity configurations are rather limited. The good news is that for any irreducible capacity configuration an intuitive generalization of the TTC rule, which we called the Circulation Top Trading Cycle (cTTC) rule, satisfies all three properties, and in fact turned out to be the unique rule to do so. We obtained a characterization for any possible capacity configuration in case preferences are “lexicographic,” which means that each agent aims to first maximize the number of units of her most preferred service, then to maximize the number of units of her second-most preferred service, etc. Our characterization on the domain of lexicographic preferences says that the cTTC rule is the unique individually rational rule that is Pareto-efficient and “dropping-proof.” Dropping-proofness (Kojima and Pathak, 2009) means that the rule cannot be manipulated by preference misrepresentations that respect the relative order of services that are listed, i.e., if the rule can be gamed by an agent then she necessarily has to recur to an arguably complicated strategy. In other words, while dropping-proofness does not exclude the possibility of profitable manipulation, it does impose a cognitive barrier.

Andersson et al. (2018) also studied time banks. They considered dichotomous preferences over individual services (i.e., a service is either acceptable or unacceptable) and extended them to bundles in a specific way. In particular, agents have upper quotas representing their maximum needs for each service. A bundle is acceptable if it does not contain unacceptable services nor exceed any upper quota. Finally, in stark contrast to Biró et al. (2018), acceptable bundles are purely evaluated according to the number/units of (acceptable) services they contain. Andersson et al. (2018) introduced so-called priority mechanisms that select individually rational circulations that are Pareto-efficient and maximize exchanges. The main result is that priority mechanisms are strategy-proof.

Finally, Manjunath and Westkamp (2018) studied a closely related framework inspired by the problem of shift-reallocation. An example is a medical practice that makes a shift plan for its doctors that at a later stage requires re-optimization based on (possibly updated) preferences. Equivalently, the problem can be formulated in terms of exchange of heterogeneous goods without monetary compensations. The main novelty of their model is the assumption that each agent has “trichotomous” preferences in the sense that she (i) partitions goods into desirable and undesirable ones, (ii) considers a bundle unacceptable if it contains undesirable goods that she was not already endowed with, and (iii) ranks acceptable bundles by their numbers of desirable goods. This assumption allowed them to introduce, similarly to Andersson et al. (2018), so-called Individually Rational Priority (IRP) rules and show that they are individually rational, Pareto-efficient, and strategy-proof.

The main take away is that designing appropriate rules for time banks is possible, but only under certain combinations of specific conditions on quotas, capacities, or, more generally, preferences. Interestingly, in the three studies that were discussed above, relatively “simple” rules do the job.
 

References: